

If you've followed the logic thus far, you might wonder, "Was this trip really necessary?" The answer: yes, because subnetting lets you split a single network address into many subnets. This is also why slash notation is so nice (no binary-to-decimal conversions). You can find such "cheats" all over the Web, including these: Converting the binary into decimal can get tricky, so it's nice to have a calculator or computer program that does the math for you, or a table. For example, the decimal representation for /16 becomes 255.255.0.0.
HOW TO FIND SUBNET MAGIC NUMBER FULL
If you'll recall Corey's article, a full byte with all eight bits turned on (11111111) adds up to a value of 255 (128 + 64 + 32 + 16 + 8 + 4 + 2 + 1), so when subnet masks are expressed in decimal, you'll often see some 255s. Though your OS uses binary bits internally, your OS permits you to specify the subnet mask in decimal or in slash notation. You don't have to go through the painful labor of calculating binary every time you want to specify a subnet. Using this Boolean logic, combining our sample IP address (192.168.1.0) with our sample subnet mask (/26) produces this result: 11000000.10101000.00000001.00000000Ĭonvert the answer back to decimal, and you still have 192.168.1.0 - but because you've specified a non-standard subnet mask, your OS now understands that this is 192.168.1.0/26, and that this network's range is 64 addresses rather than 256.

HOW TO FIND SUBNET MAGIC NUMBER PLUS
The truth plus anything false is no longer the truth. If that's hard to wrap your head around, think of 1 as "true" and zero as "false." The truth plus more truth equals truth. Without plunging deep into math theory - in other words, defer knowing "why" - let's stipulate that in this operation, 1 + 1 = 1, and 1 + = 0. The hard way is to imagine how your operating system does this: by using a CPU operation known as a Logical or Binary AND. The easy way to understand masking is to count the number of one bits in the subnet mask, because that is how many bits of the IP address will become the network portion. Your computer uses this subnet mask to "mask off" the network portion of the address, reminiscent of the way an usher in a theater might put velvet ropes around rows of seats reserved for a large group. To change a Class C address (or any class of address) into a classless CIDR address, you supply a subnet mask which differs from the "classful" default subnet mask. So if you want a /26 address, you want 26 bits of the IP address to indicate the network and 6 bits for indicating host addresses, written like this: 11111111.11111111.11111111.11000000 Zeros indicate the host portion of the address. The subnet mask is simply a binary value that uses ones to represent how many bits (out of the 32-bit IP address) represent the network portion of the address. (If you don't understand where we got that value, see Corey's article.) To understand how a subnet mask works, we have to go back to binary, because that's what your computers understand.
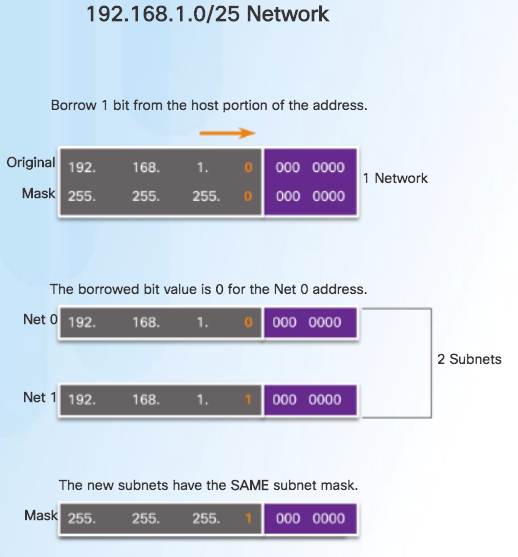
But in this case, you are seizing control by specifying one that differs from the Class C default. How do you, the administrator, impose your iron will upon IP addressing? By specifying a subnet mask. But suppose you don't want 192.168.1.0 to be a /24 network. If you use an address in the Class C range, say 192.168.1.0, your operating system will automatically think of it as a /24 address: the first three bytes indicate a network address. But newer addressing techniques, aimed at stretching the finite number of addresses available to the ever-growing Internet, now allow an IP address to be split anywhere within its 32 bits.īecause of the history of TCP/IP, your operating system (which provides you with TCP/IP) still expects you to use the old Class system. This split between the network and host portions of the address formerly occurred predictably, on full-byte boundaries. In Part 1, I explained how an IP address is really two addresses in one: part of it is a network address, and part of it is a host address. By Rik Farrow and Scott Pinzon, with updates by Corey Nachreiner


 0 kommentar(er)
0 kommentar(er)
